快速排序是一种简单的,常用(被问到)的排序算法。这里讲述一下快速排序的逻辑原理和Java的实现代码。
快速排序的思想核心,我认为就是4个字:化繁为简。
快速排序(英语:Quicksort),又称划分交换排序(partition-exchange sort),简称快排,一种排序算法,最早由东尼·霍尔提出。在平均状况下,排序n个项目要$O(n \log n )$(大O符号)次比较。在最坏状况下则需要$O(n^2)$次比较,但这种状况并不常见。事实上,快速排序通常明显比其他$O(n \log n )$演算法更快,因为它的内部循环(inner loop)可以在大部分的架构上很有效率地达成。
以上文字摘自wikiwand-快速排序
快速排序的原理
- 在一个数组中选择一个基准。将所有的元素与这个基准比较,分成大于基准条件,小于基准条件,以及如果有重复的话,还有一个等于基准条件的三个列表。
- 将大于、小于基准的两个列表重复这个操作。直到拆解的数组剩余0或1个元素。
- 将所有拆分的数组,按照顺序进行合并。
2、3步骤听起来很麻烦,其实如果使用递归的方式来实现这个问题,将会非常简单明了。
首先,我们先理解快速排序的方法和原理。
假设,我们有一个数组,数组内容为{4,5,3,2,1,6,3}7个元素,并且有一个重复的值。
我们找一个基准条件,方便起见,我在这里使用第一个元素作为基准值。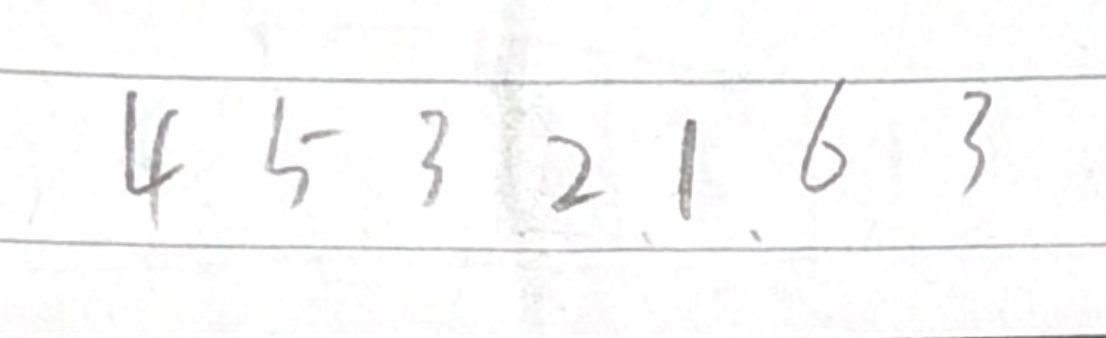
依次将每个元素与第一个元素比较,比他小的放到第一个集合,与他相同的放到第二个集合,大于他的放到第三个集合。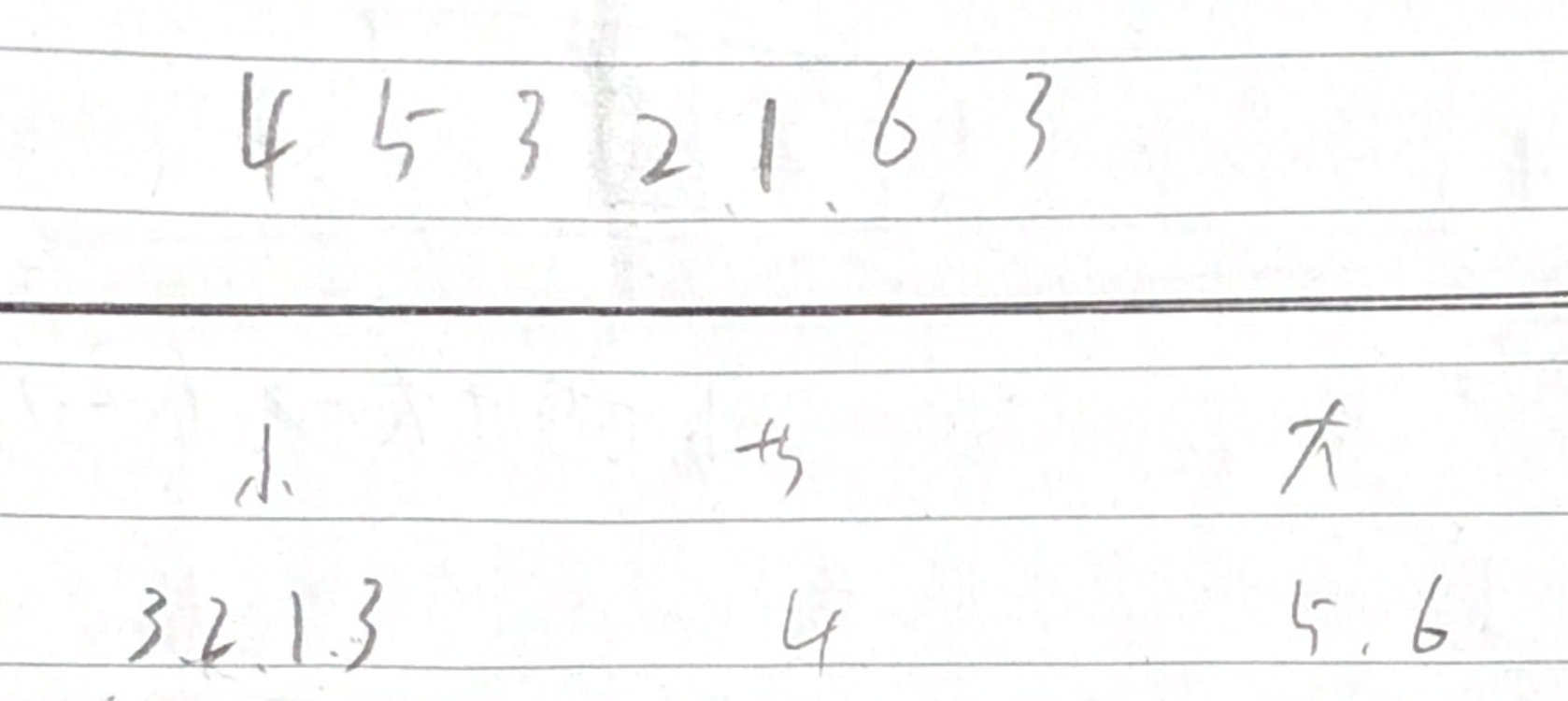
这时,将第1、3个集合继续拆分。进行无限重复,直到每个集合都只剩下0个或1个元素。
然后开始合并数据返回。
当集合元素小于2时,就不进行拆分了直接向上返回。返回的时候,将三个数组合并起来。
首先,是最底下第四层的数组,1,2都只有一个元素,合并后返回上层(1,2)。第三层左边,三个数组中,比基准小的数组就完成了排序。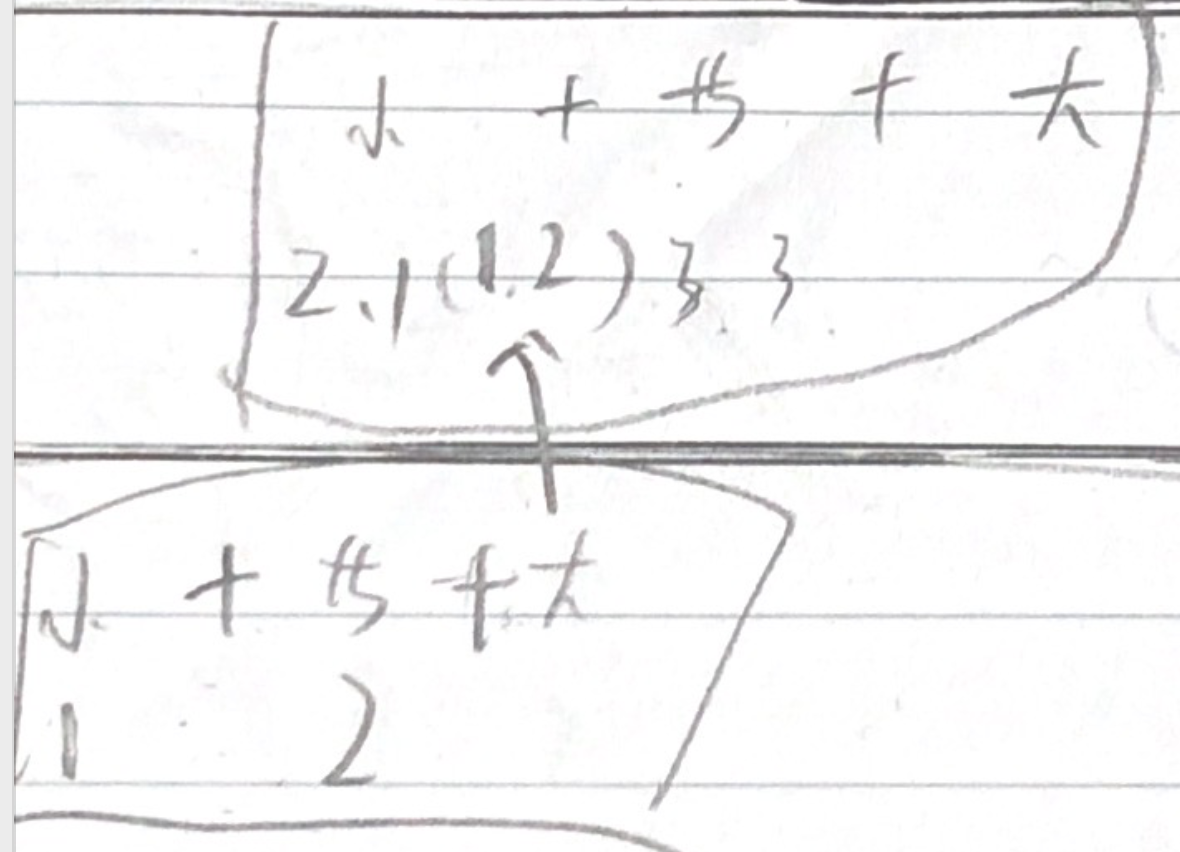
然后,第三层左侧的三个数组继续合并,向上返回(1,2,3,3),然后同样合并右侧三个数组,返回(5,6)。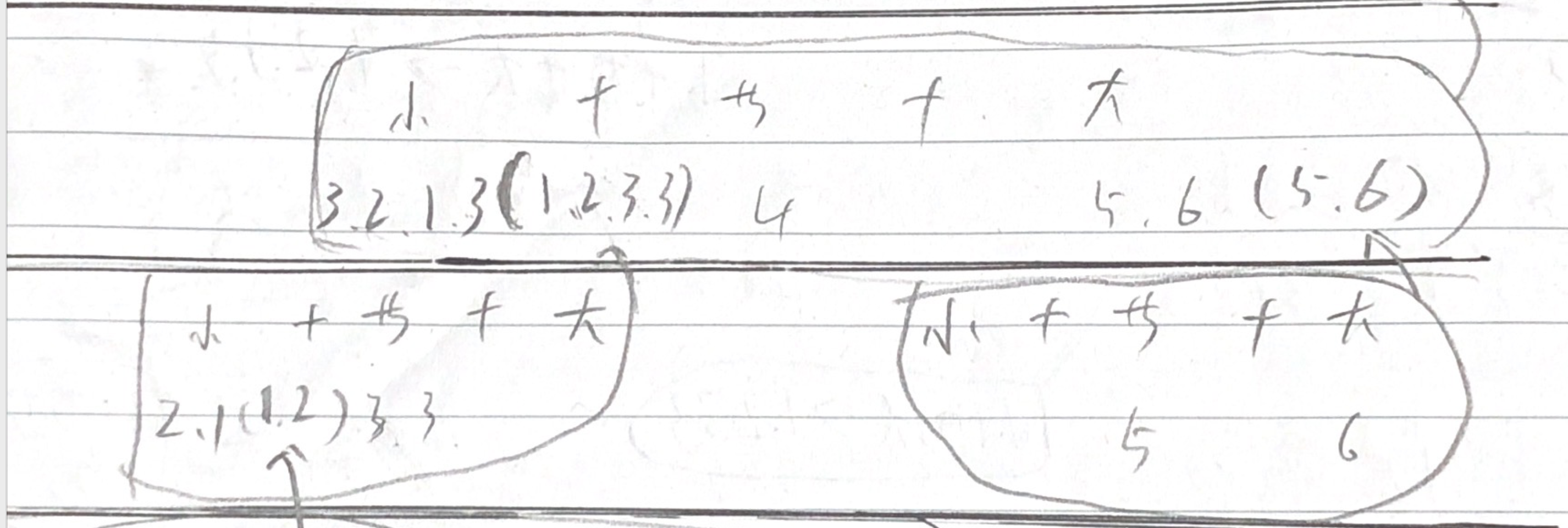
第二层的左右两个数组都完成了排序,然后三个数组合并返回(1,2,3,3,4,5,6)。完成对整个数组的排序。
字丑请见谅😝😝😝😝
将数组无限分割,直到每个数组都只有1个或0个元素,再将其合并,就完成了数组排序。下面是Java对上图的实现代码。
public static List<Integer> sequence(List<Integer> list) {
if (list.size() <= 1) return list;
List<Integer> alist = new ArrayList<>();
List<Integer> blist = new ArrayList<>();
List<Integer> clist = new ArrayList<>();
List<Integer> dlist = new ArrayList<>();
Integer i = list.get(0);
list.forEach(integer -> {
if (integer < i) alist.add(integer);
else if (integer > i) blist.add(integer);
else clist.add(integer);
});
dlist.addAll(sequence(alist));
dlist.addAll(clist);
dlist.addAll(sequence(blist));
return dlist;
}
List<Integer> list = Arrays.asList(4,5,3,2,1,6,3);
sequence(list).forEach(System.out::println);上述代码只是帮助理解快速排序,绝对不能用到实际项目中。如果因为这段代码被群殴,本人概不负责23333
快速排序的执行速度介于$O(n \log n )$ 至 $O(n^2)$之间。原理也很简单,当每一次取到的基准值都是完美的中间值,左右两个数组会等分原来的数组,数组拆分的深度就会降低($\log n$次)。当每一次取到的基准值都是集合的最大或最小值是,左右两个集合总有一个是空的。这个拆分的深度就等于数组的长度($n$次)。
本文描述的场景包括数据中可能出现重复数据的情况。查了一部分资料,理论描述中不包括重复的数组的情况。这里可能描述的有一些出入,不过思想是一致的。年轻人,研究算法不要太拘泥于形式嘛,*的思想才是重要的嘛。
化繁为简。简单的四个字并不容易做到,无论生活还是工作,这四个字都能给我们很大的帮助。学会复杂问题简单化,是每个做技术的人有应该有的基本能力。



